Lambert Theisen
Dr. rer. nat.
→ Computational Engineer, Applied Mathematician, Digital Creator.
@ RWTH Aachen University / University of Stuttgart

Blog
2023-09-05 Publishing Reproducible Numerics: A Student's Perspective 2023-06-13 Empfehlungssysteme und Matrixzerlegungen (GER) 2023-05-09 Analyse des Google PageRank Algorithmus (GER) 2023-01-06 Preconditioner for linear solvers (Markdown test) 2022-10-01 I moved to Stuttgart (during the week).Research Interest & Projects
Journal Publications & Preprints
Preprint




In this study, we present a finite element solver for a thermodynamically consistent electrolyte model that accurately captures multicomponent ionic transport by incorporating key physical phenomena such as steric effects, solvation, and pressure coupling. The model is rooted in the principles of non-equilibrium thermodynamics and strictly enforces mass conservation, charge neutrality, and entropy production. It extends beyond classical frameworks like the Nernst-Planck system by employing modified partial mass balances, the electrostatic Poisson equation, and a momentum balance expressed in terms of electrostatic potential, atomic fractions, and pressure, thereby enhancing numerical stability and physical consistency. Implemented using the FEniCSx platform, the solver efficiently handles one- and two-dimensional problems with varied boundary conditions and demonstrates excellent convergence behavior and robustness. Validation against benchmark problems confirms its improved physical fidelity, particularly in regimes characterized by high ionic concentrations and strong electrochemical gradients. Simulation results reveal critical electrolyte phenomena, including electric double layer formation, rectification behavior, and the effects of solvation number, Debye length, and compressibility. The solver's modular variational formulation facilitates its extension to complex electrochemical systems involving multiple ionic species with asymmetric valences.
Keywords: Electrochemistry, Electrical double layer, Thermodynamics, Electrolyte models, FEniCS, Finite element method
Preprint



In this work, we explore the method of fundamental solutions (MFS) for solving the regularized 13-moment (R13) equations for rarefied monatomic gases. While previous applications of the MFS in rarefied gas flows relied on problem-specific fundamental solutions, we propose a generic approach that systematically computes the fundamental solutions for any linear moment system without predefined source terms. The generalized framework is first introduced using a simple example involving the Stokes equations, and is then extended to the R13 equations. The results obtained from the generic MFS are validated against an analytical solution for the R13 equations. Following validation, the framework is applied to the case of thermally-induced flow between two non-coaxial cylinders. Since no analytical solution exists for this case, we compare the results obtained from the MFS with those obtained from the finite element method (FEM). To further assess computational efficiency, we analyze the runtimes of the FEM and MFS. The results indicate that the MFS converges faster than the FEM and serves as a promising alternative to conventional meshing-based techniques.
Keywords: regularized 13-moment equations, fundamental solution, method of manufactured solutions, finite element method
Preprint

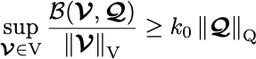
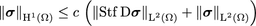
In this paper, we finally catch up with proving the well-posedness of the linearized R13 moment model, which describes, e.g., rarefied gas flows. As an extension of the classical fluid equations, moment models are robust and have been frequently used, yet they are challenging to analyze due to their additional equations. By effectively grouping variables, we identify a 2-by-2 block structure, allowing the analysis of the well-posedness within the abstract LBB framework of saddle point problems. Due to the unique tensorial structure of the equations, in addition to an interesting combination of tools from Stokes' and linear elasticity theory, we also need new coercivity estimates for tensor fields. These Korn-type inequalities are established by analyzing the symbol map of the symmetric and trace-free part of tensor derivative fields. Together with the corresponding right inverse of the tensorial divergence, we obtain the existence and uniqueness of weak solutions.
Keywords: regularized 13-moment equations, well-posedness, Korn inequalities, coercivity estimates, ellipticity, saddle point problem
SIAM Journal on Scientific Computing Vol. 46, Iss. 5 (2024)
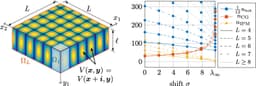
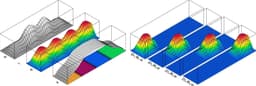


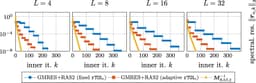
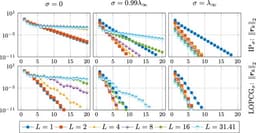
Accelerating iterative eigenvalue algorithms is often achieved by employing a spectral shifting strategy. Unfortunately, improved shifting typically leads to a smaller eigenvalue for the resulting shifted operator, which in turn results in a high condition number of the underlying solution matrix, posing a major challenge for iterative linear solvers. This paper introduces a two-level domain decomposition preconditioner that addresses this issue for the linear Schrödinger eigenvalue problem, even in the presence of a vanishing eigenvalue gap in non-uniform, expanding domains. Since the quasi-optimal shift, which is already available as the solution to a spectral cell problem, is required for the eigenvalue solver, it is logical to also use its associated eigenfunction as a generator to construct a coarse space. We analyze the resulting two-level additive Schwarz preconditioner and obtain a condition number bound that is independent of the domain's anisotropy, despite the need for only one basis function per subdomain for the coarse solver. Several numerical examples are presented to illustrate its flexibility and efficiency.
Keywords: Schrödinger equation, iterative methods, preconditioning, domain decomposition, coarse spaces, finite element method
SIAM Journal on Numerical Analysis Vol. 60, Iss. 5 (2022)
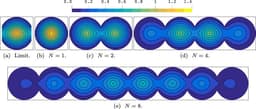
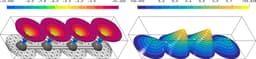
This paper provides a provably quasi-optimal preconditioning strategy of the linear Schrödinger eigenvalue problem with periodic potentials for a possibly nonuniform spatial expansion of the domain. The quasi-optimality is achieved by having the iterative eigenvalue algorithms converge in a constant number of iterations for different domain sizes. In the analysis, we derive an analytic factorization of the spectrum and asymptotically describe it using concepts from the homogenization theory. This decomposition allows us to express the eigenpair as an easy-to-calculate cell problem solution combined with an asymptotically vanishing remainder. We then prove that the easy-to-calculate limit eigenvalue can be used in a shift-and-invert preconditioning strategy to bound the number of eigensolver iterations uniformly. Several numerical examples illustrate the effectiveness of this quasi-optimal preconditioning strategy.
Keywords: periodic Schrödinger equation, iterative eigenvalue solvers, preconditioner, asymptotic eigenvalue analysis, factorization principle, directional homogenization
ACM Trans. Math. Softw. 47, 2, Article 17 (April 2021)


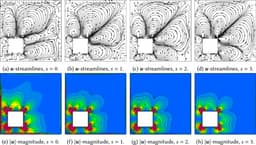
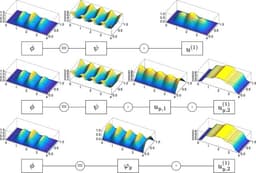
We present a mixed finite element solver for the linearized regularized 13-moment equations of non-equilibrium gas dynamics. The Python implementation builds upon the software tools provided by the FEniCS computing platform. We describe a new tensorial approach utilizing the extension capabilities of FEniCS’ Unified Form Language to define required differential operators for tensors above second degree. The presented solver serves as an example for implementing tensorial variational formulations in FEniCS, for which the documentation and literature seem to be very sparse. Using the software abstraction levels provided by the Unified Form Language allows an almost one-to-one correspondence between the underlying mathematics and the resulting source code. Test cases support the correctness of the proposed method using validation with exact solutions. To justify the usage of extended gas flow models, we discuss typical application cases involving rarefaction effects. We provide the documented and validated solver publicly.
Keywords: tensorial mixed finite element method, R13 equations, FEniCS project, continuous interior penalty
Talks
- Scalable Domain Decomposition Eigensolvers for Schrödinger Operators in Anisotropic Structures, PhD Thesis Defense, Aachen (Germany), 13 June, 2024.
- Scalable Domain Decomposition Eigensolvers for Schrödinger Operators in Anisotropic Structures, Lothar Collatz Seminar at RTG 2583: Modeling, Simulation and Optimization of Fluid Dynamic Applications, Hamburg (Germany), 29 May, 2024.
- Publishing Reproducible Numerics: A Student's Perspective, Research Data Management (RDM) Workshop at SFB 1481: Sparsity and Singular Structures, Aachen (Germany), 05 September, 2023.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, 29th Biennial Conference on Numerical Analysis, Glasgow (Scotland), 27 June, 2023.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, Workshop on Numerical Analysis of Nonlinear Schrödinger Equations, Augsburg (Germany), 22 June, 2023.
- Robust Solvers for the Schrödinger Eigenvalue Problem with Long-Range Inter- actions in Anisotropically Expanding Domains, GAMM 93rd Annual Meeting. Section S26: Modeling, Analysis, and Simulation of Molecular Systems, Dresden (Germany), 01 June, 2023.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, EMC2 Seminar (ERC Synergy project - Extreme-scale Mathematically-based Computational Chemistry), Paris (France), 10 March, 2023.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, SIAM Conference on Computational Science and Engineering (CSE23), Amsterdam (Netherlands), 28 February, 2023.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, IANS Oberseminar, University of Stuttgart, Stuttgart (Germany), 24 November, 2022.
- A Two-Level Domain Decomposition Method for Periodic Schrödinger Eigenstates in Anisotropically Expanding Domains, DD27: 27th International Domain Decomposition Conference – MS4: SCSs in DDMs and Multiscale Discretizations, Prague (Czech Republic), 27 July, 2022.
- A Quasi-Optimal Factorization Preconditioner for Periodic Schrödinger Eigenstates in Non-Uniformly Expanding Domains, ESCO 2022: 8th European Seminar on Computing, Pilsen (Czech Republic), 14 June, 2022.
- A Quasi-Optimal Factorization Preconditioner for Periodic Schrödinger Eigenstates in Non-Uniformly Expanding Domains, ACoM Lunch Seminar, RWTH Aachen University, Aachen (Germany), 7 June, 2022.
- An Optimal Factorization Preconditioner for Periodic Schrödinger Eigenstates in Non-Uniformly Expanding Domains, ACoM Lunch Seminar, RWTH Aachen University, Aachen (Germany), 15 June, 2021.
- Optimal Eigensolvers for Dirichlet Schrödinger Operators with Non-Negative Additively Separable Potentials in Long Domains, GAMM Activity Group: Modelling, Analysis and Simulation of Molecular Systems (MOANSI) Annual Meeting 2020, Aachen (Germany), 24-25 September, 2020.
- Optimal Eigensolvers for Dirichlet Schrödinger Operators with Non-Negative Additively Separable Potentials in Long Domains, MathCCES Lunch Seminar, RWTH Aachen University, Aachen (Germany), 30 June, 2020.
- Simulation of Non-Equilibrium Gas Flows Using the FEniCS Computing Platform, Master Thesis Defense, MathCCES Lunch Seminar, RWTH Aachen University, Aachen (Germany), 15 October, 2019.
- Shear-Slip Mesh Update Method for Compressible Flow Simulations Involving Rotating Sub-Domains, CES Seminar Presentation, RWTH Aachen University, 10 April, 2019.
- Automated Boundary Layer Mesh Generation for Simulation of Convective Cooling, Bachelor Thesis Defense, MathCCES Lunch Seminar, RWTH Aachen University, 10 April, 2018.
Open Source Software
 GeMotion.jl: A Navier-Stokes-Fourier Solver for generalized material laws.
GeMotion.jl: A Navier-Stokes-Fourier Solver for generalized material laws.- DBPrices.jl: A Julia wrapper for the db-prices module from @juliuste.
 ddEigenlab.jl: A Domain-Decomposition Eigenvalue Problem Lab to benchmark various algorithms.
ddEigenlab.jl: A Domain-Decomposition Eigenvalue Problem Lab to benchmark various algorithms. fenicsR13: A Tensorial Mixed Finite Element Solver for the Linear R13 Equations Using the FEniCS Computing Platform.
fenicsR13: A Tensorial Mixed Finite Element Solver for the Linear R13 Equations Using the FEniCS Computing Platform.- latextools: Some scripts to process LaTeX documents. Contains a conversion script for LaTeX files into plaintext while keeping the mathematical sentence structure intact. For example, the input
Let $\begin{equation} h = \tfrac{1}{N} \end{equation}$ where $N$ denotes the number of intervals.will be converted toLet noun verbs noun where noun denotes the number of intervals.(valid sentence).
Miscellaneous
- Generate pictures of arbitrary-order Lagrangian finite element basis function with the Mathematica script from 10.6084/m9.figshare.9767021.v1 (uploaded to figshare).
Theses and Supervised Work
- Density Operator in Eigenvalue Problems with Application in Manifold Interpolation, Bachelor Thesis of Stefan Berger, RWTH Aachen, 2022.
- Evaluation and Implementation of Schrödinger-Type Eigenvalue Problems in Long Rectangular Domains using the Finite Element Method, CES Project Thesis of Corinna Müller, Matthias Geratz, Celine Heger, Johanna Meyer, RWTH Aachen, 2021.
- Using a Spectral Inference Network to Solve the Time-Independent Schrödinger Equation for a Two-Dimensional Hydrogen Atom, Seminar Thesis of Alexander Kristof, RWTH Aachen, 2020.
- Iterative Domain Decomposition Methods for Eigenvalue Problems, Master Thesis of Hendrik Borchardt, RWTH Aachen, 2020.
- Simulation of Non-Equilibrium Gas Flows Using the FEniCS Computing Platform, Master Thesis of Lambert Theisen, RWTH Aachen / MathCCES, 2020.
- Shear-Slip Mesh Update Method for Compressible Flow Simulations Involving Rotating Sub-Domains, Seminar Thesis of Lambert Theisen, RWTH Aachen / CATS, 2019.
- Automated Boundary Layer Mesh Generation for Simulation of Convective Cooling, Bachelor Thesis of Lambert Theisen, RWTH Aachen / ABB Switzerland, 2018.
Teaching
You can find most of my teaching activity in the Github repository @lamBOOO/teaching.
Selected classes
Schulmathematik vom höheren Standpunkt [50% der Vorlesung]
We covered topics from the real life including: How does GPS work?; Why is the Netflix recommendation algorithm so good?; How to optimize solar plants?; What's the algorithm to detect traffic lights?; How is data compression done?; What was the idea of the initial PageRank algorithm by Google? We used the learning concept from CAMMP (https://www.cammp.online) in a workshop style and reflected the mathematical concepts from the higher perspective and how to embedded them in the mathematics class in the school .
Höhere Mathematik 1 für Ingenieure [Vortragsübung]
Linear algebra is the study of the basic concepts and techniques involving vectors and matrices. The course topics include logic, numbers and sets; vectors and vector spaces; systems of linear equations; linear transformations and their properties; eigenvalues and eigenvectors. The course objectives are to develop students’ skills in reasoning, modeling and problem-solving with vectors and matrices.
Mathematische Aspekte in der computergestützten Chemie [Vortragsübung]
This course explores the use of mathematical concepts in computational chemistry, specifically in creating and breaking down models of molecules. We will take a mathematical approach to theoretical chemistry, covering topics such as electric charge interactions between molecular systems, the transition from classical to quantum mechanics, the Hartree-Fock model, and its breakdown. If time allows, we will also examine some aspects of Density Functional Theory (DFT). By the end of the course, students will have a deep understanding of the mathematical principles underlying computational chemistry and will be able to apply these principles to their own research in the field.
Mathematische Grundlagen III (CES) [Vortragsübung]
This course introduces variational calculus, which is a branch of mathematics that deals with finding the best solution to a problem involving functions. It also teaches how to integrate functions in several variables and on different types of spaces, such as curves and surfaces. The course also covers numerical methods for solving ordinary differential equations, which are equations that relate a function and its derivatives. Moreover, the course explores optimization techniques for finding the minimum or maximum value of a function and eigenvalue computation methods for finding the characteristic values of a matrix. The course aims to help students acquire and apply these mathematical tools in various fields of science and engineering.
Mathematische Grundlagen III (CES) [Vortragsübung]
This course introduces variational calculus, which is a branch of mathematics that deals with finding the best solution to a problem involving functions. It also teaches how to integrate functions in several variables and on different types of spaces, such as curves and surfaces. The course also covers numerical methods for solving ordinary differential equations, which are equations that relate a function and its derivatives. Moreover, the course explores optimization techniques for finding the minimum or maximum value of a function and eigenvalue computation methods for finding the characteristic values of a matrix. The course aims to help students acquire and apply these mathematical tools in various fields of science and engineering.
Mathematische Grundlagen IV (CES) [Vortragsübung]
In this course, students will explore the theory and numerics of partial differential equations (PDEs), which are mathematical models of phenomena involving rates of change in multiple variables. The course will cover various aspects of PDEs, such as their classification by type and basic characteristics, their elementary solution methods for some classical examples, their generalization by using distributions and Sobolev spaces to define weak derivatives, their analysis by applying Fourier and other integral transformations to different domains, their discretization by finite difference methods on grids, and their numerical solution by efficient techniques such as FFT or filtering. The course will combine theoretical lectures with practical exercises using MATLAB or Julia.
Mathematische Grundlagen I (CES) [Vortragsübung]
In this course, you will learn about various aspects of linear algebra and analysis of functions of several variables. You will explore how to solve eigenvalue problems and transform matrices into diagonal or normal forms. You will also learn how to use singular value decomposition, rank determination and regularization concepts. You will apply differentiation, Taylor expansion, inverse and implicit functions to analyze and optimize multivariable functions. You will use iterative methods such as Newton’s method or Gauss-Newton method to solve nonlinear systems of equations and least squares problems. You will understand how to interpolate data using polynomials and how to perform numerical differentiation and integration using Newton-Cotes formulas, Gauss quadrature and extrapolation. Finally, you will get an introduction to the theory of ordinary differential equations.
Mathematische Grundlagen IV (CES) [Tutor]
I executed the self exercise and supervised students in the course on partial differential equations (PDEs). I learned and applied the theory and numerics of PDEs, such as their types, characteristics, solutions, generalizations, analysis, discretization and numerical solution. I also helped the students understand and practice these concepts and methods using MATLAB or Julia.
Partielle Differentialgleichungen (CES) [Tutor]
This course covers various aspects of the variational formulation for elliptic problems, such as the Galerkin technique and the Lax-Milgram theorem. It also introduces the finite element method for elliptic problems and some modern iterative methods, such as PCG and multigrid method. The course then extends to parabolic problems and shows how to use the method of lines for their discretization. It also presents the finite volume method as another discretization technique. The course then deals with saddle point problems and their application to Stokes equations. Finally, it discusses the Navier-Stokes equation for incompressible fluids. The main goals of this course are to help students understand the basic principles of discretizing partial differential equations and to teach them how to use different numerical methods for solving them. The students will also learn how to evaluate the results of these methods and how to adapt them to new tasks. The students will acquire confidence in using discretization techniques such as finite elements and finite volume methods, as well as iterative solution methods such as PCG and multigrid method.
Selected Projects
 The tool gradescaler.com provides a graphical overview of exam grading schemes.
The tool gradescaler.com provides a graphical overview of exam grading schemes.- Use the shopping-list LaTeX template to create your 4x4 double-sided reusable shopping list for easy ticking of required products based on the supermarket location to optimize shopping. Here's an example.
- A while ago, I build the website kanara-bau.de without using any tech stack in the editor.
Contact
You can contact me directly via the e-mail address lmbrt∂thsn.dev or lambert.theisen∂rwth-aachen.de preferrable using PGP encryption. My PGP key can be found on the keyserver keys.openpgp.org or you can directlty download it here using the link lt-pgpkey.asc. The corresponding signature reads 9C32 B2D9 E59B 09C1 72AB C577 F2C2 52C0 F331 EB87.
 Protocol
Protocol
You can also contact me via the Matrix protocol, which is an open-source, end-to-end encrypted and decentralised messaging service. Simply hit @lamboo:matrix.org and start texting me.
Profiles
I am part of the major science and networking sites, for example:
Also have a look at my institute webpages:
Impressum
Applied and Computational Mathematics (ACoM)
RWTH Aachen University
Schinkelstr. 2, Room 229 (Rogowski Building, 2nd floor)
52062 Aachen
Germany
Office Phone: 0049 241 80-98671
Mobile Phone: 0049 241 80-98686
Institut für Angewandte Analysis und Numerische Simulation (IANS)
Lehrstuhl Numerische Mathematik für Höchstleistungsrechner (NMH)
Universität Stuttgart
Pfaffenwaldring 57, Raum 7.154
70569 Stuttgart
Germany
Office Phone: 0049 711 685 65522
